UNIDAD ACADÉMICA DE INGENIERÍA
INGENIERO CIVIL
GRADO: 2º GRUPO: 401
UNIDAD DE APRENDIZAJE:
MÉTODOS NUMÉRICOS
DOCENTE:
LORENA ALONSO GUZMAN
TEMA: SECUENCIA 4°
ALUMNO: SAMUEL SANTOS
MORENO
TURNO: MATUTINO
CHILPANCINGO DE LOS BRAVOS. GRO; A, 11 DE
JUNIO DEL 2018
I.
INDICE DE CONTENIDO
Contenido
I. Introducción
2. Integración y diferenciación numérica
3. Método del trapezoidal
4. Ejercicios
5. Métodos de newton-cotes
6. Método trapezoidal compuesto
7. Método de Simpson 1/3
8. Regla de Simpson 3/8
9. Cuadratura de Gauss
9.1. Formula de cuadratura de Gauss con
dos puntos
10. Diferenciación numérica
11. conclusión
12. Bibliografía
I. INTRODUCCIÓN
En
esta competencia se abordarán los temas clásicos de integración definida y de
evaluación de derivadas en algún punto, por medio de técnicas numéricas. Para
ello se utilizarán procesos finitos, en los que, a diferencia de los métodos
analíticos, donde el concepto de límite es central y por tanto los procesos
infinitos- se manejan conjuntos de puntos discretos y haremos pasar por ellos o
entre ellos un polinomio, para después integrar o derivar dicho polinomio.
Ya que son números básicos, para escribir en los programas
y resolverlos en una computadora y usar correctamente el software existente
para dichos métodos. El análisis numérico trata de diseñar métodos para
“aproximar” de una manera eficiente las soluciones de problemas expresados
matemáticamente.
En la mayoría
de los casos, sin embargo, no se puede utilizar esta fórmula, ya que no se
conoce dicha primitiva. Es posible, por ejemplo, que no se conozca la expresión
matemática de la función f, sino solo sus valores en determinados puntos. Pero
también hay funciones (de apariencia sencilla) para las que se puede demostrar
que no tienen ninguna primitiva que pueda escribirse en términos de funciones.
La integración
numérica es una herramienta de las matemáticas que proporciona fórmulas y
técnicas para calcular aproximaciones de integrales definidas. Gracias a ella
se pueden calcular, aunque sea de forma aproximada, valores de integrales
definidas que no pueden calcularse analíticamente y, sobre todo, se puede
realizar ese cálculo en un ordenador.
El objetivo
principal de Integración y diferenciación numérica es como encontrar soluciones
“aproximadas” a problemas complejos utilizando sólo las operaciones, se
requiere de una secuencia de operaciones algebraicas y lógicas que producen La
aproximación al problema matemático.
Para quedar en la nueva
rotación
x0= a
xn= b
2)
se aproxima eje x por un
polinomio pn (x) y se integra para tener la aproximación de I.
3.
Método del trapezoidal
en el caso de n=1 el intervalo
de integración [ a, b] queda tal cual:
x0=a
xi=b,
la aproximación de f(x) es una
línea recta y la aproximación o la integral es el área del trapezoide bajo esta
línea recta.
Procedimientos.
Actividades
a)
xo= 0
xi=5
n=6
h= 5/6= 1
Ejercicio
F(x) = e2x
PARA DOS PUNTOS
X0=1.1
h= 0.1
X0+h=1
X0+2h=1.3
INTRODUCCIÓN
La
integración numérica es una herramienta esencial que se usa en la ciencia y en
la ingeniería para obtener valores aproximados de integrales definidas que no
pueden calcularse analíticamente.
Para
quedar en la nueva notación 𝑥0
= 𝑎 y 𝑥𝑛
= 𝑏
2.
Se aproxima 𝑓(𝑥) por un polinomio de
grado n; 𝑃𝑛(𝑥) y se integra para
obtener la aproximación de I.
Es
evidente que se obtendrán valores diferentes de I para distintos valores de n,
como se muestra a continuación.
MÉTODO TRAPEZOIDAL
En
el caso de n = 1, el intervalo de integración [a, b] queda tal cual y 𝑥0 = 𝑎, 𝑥1 = 𝑏; la aproximación
polinomial de f(x) es una línea recta (un polinomio de primer grado p(x)) y la
aproximación a la integral es el área de trapezoide bajo esta línea recta, como
se ve en la figura. Este método de integración se llama regla trapezoidal.
6. MÉTODO TRAPEZOIDAL COMPUESTO
En
vez de aproximar la integral de f(x) en [a, b] por una recta, conviene dividir
[a, b] en n subintervalos y aproximar cada uno por un polinomio de primer grado.
Ejemplo:
f (x) =x4-2x2+x+10
a
|
-1
|
||||||
b
|
4
|
||||||
n
|
1
|
||||||
i
|
XI
|
XΛ4
|
2XΛ2
|
X
|
10FXI
|
||
0
|
-1
|
1
|
-2
|
-1
|
10
|
8
|
|
1
|
0
|
0
|
0
|
0
|
10
|
10
|
|
2
|
1
|
1
|
-2
|
1
|
10
|
10
|
|
3
|
2
|
16
|
-8
|
2
|
10
|
20
|
|
4
|
3
|
81
|
-18
|
3
|
10
|
76
|
|
23
|
|||||||
5
|
4
|
256
|
-32
|
4
|
10
|
8
|
239
|
Se aproxima f(x) con una parábola [un polinomio de segundo
grado pix)], y la aproximación a la integral será el área bajo el segmento de
parábola comprendida entre f(xo) y f(x2). Esto es:
Con
la regla de Simpson 3/8 integre: 𝑓
𝑥 = 0.2 + 25𝑥 − 200𝑥2
+ 675𝑥3
− 900𝑥4
+ 400𝑥5,
desde a= 0 hasta b= 0.8, con n=2 y n=3, este ejercicio está resuelto para n=3
Úsela
junto con la regla de Simpson 1/3 con la finalidad de integrar la misma función
en cinco segmentos.
Una
sola aplicación de la regla de Simpson 3/8 requiere cuatro puntos equidistantes
𝑥0 = f(0)=0.2
𝑥1
= 𝑓 0.2667 = 1.432724
𝑥2 = 𝑓 0.5333 = 3.487177
𝑥3 = 𝑓 0.8 =0.232
DONDE SE HAN CALCULADO LOS VALORES Wi Y
Z, EN LA TABLA, LA CUAL DA VALORES HASTA PARA SEIS PUNTOS.
Esta
simple formula es exacta si F es un polinomio de grado menor o igual a tres.
Para otra f es una aproximación equivalente a sustituir f con un polinomio de
grado tres.
10. DIFERENCIACIÓN NUMÉRICA
La
derivada de una función tiene muchas aplicaciones, entre las cuáles esta la
determinación de la velocidad instantánea de una partícula o móvil a partir de
su función de posición. Este proceso es en ocasiones algo muy sencillo cuando
se cuenta con dicha función, pero cuando se requiere solucionar el mismo
problema con un conjunto de datos discretos y no con su función, el
procedimiento no puede ser llevado de igual manera, es decir, el cálculo no nos
da una solución directa, por lo tanto, se debe recurrir a otro tipo de
análisis.
Notaremos
la aproximación a la derivada de una función f como f’
Nota:
Esta fórmula, aunque sencilla no tiene un comportamiento estable, ya que para
funciones lineales puede llegar a ser exacta, no siendo así para funciones más
generales. Pero sin duda alguna, es un buen punto de partida para el calculo de
la derivada de una función, además hay que considerar que en algunos casos es
la única opción con que se cuenta.
LA TABLA A CONTINUACIÓN RESUME LAS FÓRMULAS PARA
APROXIMACIÓN DE LAS DERIVADAS.
LA
TABLA A CONTINUACIÓN RESUME LAS FÓRMULAS PARA APROXIMACIÓN DE LAS DERIVADAS.
SEGUNDA DERIVADA
SEGUNDA DERIVADA
EJEMPLO:
Aproximar la primera derivada de la función 𝑓
𝑥 = 𝑒2𝑥,
con todas las fórmulas que se encuentran en las tablas para un X0= 1.1 y h=0.1,
use el hecho de que f’(1.1)=18.050, para el cálculo del error absoluto
Solución:
Se
requieren los valores de:
𝑓(𝑥0), 𝑓 𝑥0 + ℎ 𝑦
𝑓 𝑥0 + 2ℎ
𝑓(𝑥0):𝑓 1.1 = 9.025
𝑓 𝑥0 + ℎ :𝑓
1.2 = 11.023
𝑓 𝑥0 + 2ℎ :𝑓
1.3 = 13.464
Usando
las fórmulas de diferencias finitas progresivas:
11.
CONCLUSIÓN
En estas notas hemos discutido
algunos métodos clásicos para aproximar integrales, así como algunas de las
técnicas de integración desarrollados durante los últimos años: aproximaciones
analíticas, integración numérica, métodos trapezoidales de integración y
diferenciación numérica, la elección depende, por supuesto, del tipo de
información que se requiera en cada aplicación específica.
Los métodos de Simpson 1/3 son
bastante flexibles en relación con los otros métodos, pero pueden llegar a
tener un costo computacional muy alto. Probablemente la mejor estrategia en una
aplicación concreta consista en combinar varios de los métodos revisados en
estas notas. Es frecuente, por ejemplo, que la aproximación normal asintótica a
la distribución final del parámetro de interés sugiera formas que pueden ser
utilizadas como distribuciones de muestreo por importancia para la fórmula de
cuadratura de Gauss, o bien como distribuciones de transición para el algoritmo
de diferenciación numérica.
En términos generales, las
técnicas aquí discutidas serán más eficientes y darán resultados más precisos
en la medida en que la aproximación normal asintótica a la distribución final
sea más adecuada. Es por esta razón que en la mayoría de los casos resulto es conveniente
trabajar en términos de una Re parametrización del modelo, de manera que cada
uno de los nuevos parámetros tome valores en toda su distribución final sea
aproximadamente normal. En el caso de algunos procedimientos, tales como las
reglas Simpson 3/8, de integración numérica o el método trapezoidal compuesto, son
de gran valor para utilizarlo en los procedimientos. también es importante que
la correlación final entre los nuevos parámetros no sea muy alta.
Finalmente, cabe señalar que las
nuevas técnicas como las de reglas Simpson 3/8, de integración numérica ha
permitido el desarrollo de software para analizar modelos cada vez más
complejos.
12.
BIBLIOGRAFÍA






































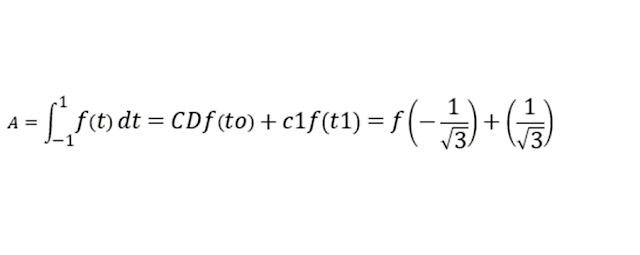







No hay comentarios:
Publicar un comentario