UNIDAD ACADÉMICA DE INGENIERÍA
INGENIERO CIVIL
GRADO: 2º GRUPO: 401
UNIDAD DE APRENDIZAJE:
MÉTODOS NUMÉRICOS
DOCENTE:
LORENA ALONSO GUZMAN
TEMA: COMPETENCIA 3°
ALUMNO: SAMUEL SANTOS
MORENO
TURNO: MATUTINO
CHILPANCINGO DE LOS BRAVOS. GRO; A, 28 DE MAYO
DEL 2018
ÍNDICE DE
CONTENIDO
Contenido
1. Introducción
2. Sistema de
ecuaciones lineales
3. Tipos de sistemas lineales
3.1. Sistema
compatible
3.2
Sistema compatible determinado
3.3
Sistemas compatibles indeterminados
3.4.
Sistema incompatible
4. Resolución de sistemas de ecuaciones
lineales
4.1
Igualación
4.2
Reducción
5. Método grafico
6. Método de Gauss
7. Eliminación de Gauss-Jordán
8. Regla de Cramer
9. Operaciones de matrices
9.1. Producto interno de matrices
10. Inversa de una matriz
11. Actividades
12. Regla de Cramer
13. Descomposición LU
14. Método de
gauss-Seidel
15. Matrices y sistemas de ecuaciones lineales
15.1. Suma de matrices
15.2. Suma de matrices por un escalar
15.3 Multiplicaciones de matrices
16 conclusión
17. Bibliografía
1. INTRODUCCIÓN
Los métodos numéricos son procedimientos por los cuales
se obtiene en su mayoría de manera aproximada la solución de ciertos problemas
realizando cálculos que son aritméticos y también en su mayoría lógicos
(operaciones de aritméticas que son elementales, cálculos de funciones, en
consulta de tablas de valores, cálculos preposicionales.
Algún procedimiento consiste en una fila que es finita de
procedimientos e instrucciones que son precisas y especifican una secuencia de
operaciones algebraicas y lógicas, que producen o bien hacen una aproximación
de la solución del problema. La eficiencia del cálculo del cálculo de la
aproximación depende, en parte, a la facilidad que se tenga el implementar el
algoritmo y de las características especiales y las limitaciones de los
instrumentos que son de cálculo.
El análisis
numérico trata de diseñar métodos para “aproximar” de una manera eficiente las
soluciones de problemas expresados matemáticamente.
Los métodos numéricos son números
que los seres humanos han ido construyendo a través del tiempo para superar las
diferentes barreras naturales con las que se han encontrado y poder así hacer
uso de los mismos con la finalidad de aplicar
las Matemáticas a situaciones del mundo real, nos encontramos a menudo con
problemas que no pueden ser resueltos analíticamente o de manera exacta y cuya
solución debe ser abordada con ayuda de algún procedimiento numérico.
Los métodos numéricos pueden clasificarse de diferentes
tipos, de acuerdo a diversos conceptos como el tipo de materias utilizado, en las
matemáticas, el sistema de ecuaciones lineales predominante a operaciones
utilizado, el uso de matrices la ubicación de reducción por el método de Gauss.
El objetivo
principal es encontrar soluciones “aproximadas” a problemas complejos
utilizando sólo las operaciones, se requiere de una secuencia de operaciones
algebraicas y lógicas que producen, la aproximación al problema matemático.
El conocimiento
y la comprensión son prerrequisitos para la aplicación eficaz de cualquier
herramienta.
2. SISTEMA DE ECUACIONES LINEALES
Sistema de ecuaciones lineales, también conocido
como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto
de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada
ecuación es de primer grado), definidas sobre un cuerpo o un anillo
conmutativo. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:
El
problema consiste en encontrar los valores desconocidos de las variables x1, x2
y x3 que satisfacen las tres ecuaciones.
El
problema de los sistemas lineales de ecuaciones es uno de los más antiguos de
la matemática y tiene una infinidad de aplicaciones, como en procesamiento
digital de señales, análisis estructural, estimación, predicción y más
generalmente en programación lineal, así como en la aproximación de problemas
no lineales de análisis numérico.
En
general, un sistema con m ecuaciones lineales y n incógnitas puede ser escrito
en forma normal como:
Si
representamos cada matriz con una única letra obtenemos:
Ax= b.
Donde
A es una matriz m por n, x es un vector columna de longitud n y b es otro
vector columna de longitud m.
El
sistema de eliminación de Gauss-Jordán se aplica a este tipo de sistemas, sea
cual sea el cuerpo del que provengan los coeficientes. La matriz A se llama
matriz de coeficientes de este sistema lineal. A b se le llama vector de
términos independientes del sistema y a x se le llama vector de incógnitas.
Sistemas lineales reales
En
esta sección se analizan las propiedades de los sistemas de ecuaciones lineales
sobre el cuerpo {R} }, es decir, los sistemas lineales en los cuales los
coeficientes de las ecuaciones son números reales.
Representación gráfica
La intersección de dos planos
que no son paralelos coincidentes es una recta.
Un sistema con [n]
incógnitas se puede representar en el n-espacio correspondiente.
En los
sistemas con 2 incógnitas, el universo de nuestro sistema será el plano
bidimensional, mientras que cada una de las ecuaciones será representada por
una recta. La solución será el punto (o línea) donde se intersequen todas las
rectas representan a las ecuaciones. Si no existe ningún punto en el que se
intersequen al mismo tiempo todas las líneas, el sistema es incompatible, o lo
que es lo mismo, no tiene solución.
En el
caso de un sistema con 3 incógnitas, el universo será el espacio
tridimensional, siendo cada ecuación un plano dentro del mismo. Si todos los
planos intersecan en un único punto, las coordenadas de este serán la solución
al sistema. Si, por el contrario, la intersección de todos ellos es una recta o
incluso un plano, el sistema tendrá infinitas soluciones, que serán las
coordenadas de los puntos que forman dicha línea o superficie.
Para
sistemas de 4 o más incógnitas, la representación gráfica no existe, por lo que
dichos problemas no se enfocan desde esta óptica.
3. TIPOS DE SISTEMAS LINEALES
Los
sistemas de ecuaciones se pueden clasificar según el número de soluciones que
pueden presentar. De acuerdo con ese caso se pueden presentar los siguientes
casos:
Sistema
compatible: si tiene solución, en este caso además puede distinguirse
entre:
Sistema
compatible determinado: cuando tiene una única solución.
Sistema
compatible indeterminado cuando admite un conjunto infinito de
soluciones.
Sistema incompatible si no
tiene solución.
Quedando
así la clasificación:
Los
sistemas incompatibles geométricamente se caracterizan por (hiper)planos o
rectas que se cruzan sin cortarse. Los sistemas compatibles determinados se
caracterizan por un conjunto de (hiper)planos o rectas que se cortan en un
único punto. Los sistemas compatibles indeterminados se caracterizan por
(hiper)planos que se cortan a lo largo de una recta [o más generalmente un hiperplano
de dimensión menor]. Desde un punto de vista algebraico los sistemas
compatibles determinados se caracterizan porque el determinante de la matriz es
diferente de cero:
Algoritmo
para determinar si un sistema es compatible
Podemos
averiguar si un sistema es o no compatible mediante el Teorema de
Rouché-Frobenius que establece que un sistema de ecuaciones lineales es
compatible sólo si el rango de su matriz ampliada coincide con el de su matriz
de coeficientes. Supongamos que el sistema es compatible.
3.2 Sistema compatible determinado
Si el
valor común de los rangos de las matrices coincide con el número de variables,
el sistema es compatible determinado; en caso contrario, es compatible
indeterminado.
Tanto
la primera como la segunda ecuación se corresponden con la recta cuya pendiente
es {-0,5} y que pasa por el punto (-1,1), por lo que ambas coinciden en todos
los puntos de dicha recta. El sistema es compatible por tener solución o puntos
comunes entre las rectas, pero es indeterminado al ocurrir esto en infinitos
puntos.
En
este tipo de sistemas, la solución genérica consiste en expresar una o más
variables como función matemática del resto. En los sistemas lineales
compatibles indeterminados, al menos una de sus ecuaciones se puede hallar como
combinación lineal del resto, es decir, es linealmente dependiente.
La condición necesaria para que un sistema sea compatible indeterminado es que el determinante de la matriz del sistema sea cero al igual que el rango de la matriz ampliada y menor al número de incógnitas (y por tanto uno de sus autovalores será 0):
De
hecho, de las dos condiciones anteriores se desprende, que el conjunto de
soluciones de un sistema compatible indeterminado es un subespacio vectorial. Y
la dimensión de ese espacio vectorial coincidirá con la multiplicidad
geométrica del autovalor cero.
3.4 Sistemas incompatibles
Las
ecuaciones se corresponden gráficamente con dos rectas, ambas con la misma
pendiente, Al ser paralelas, no se cortan en ningún punto, es decir, no existe
ningún valor que satisfaga a la vez ambas ecuaciones.
Matemáticamente
un sistema de estos es incompatible cuando el rango de la matriz del sistema es
inferior al rango de la matriz ampliada. Una condición necesaria para que esto
suceda es que el determinante de la matriz del sistema sea cero:
4. Resolución de sistemas de ecuaciones
lineales
Sustitución
El
método de sustitución consiste en despejar en una de las ecuaciones con
cualquier incógnita, preferiblemente la que tenga menor coeficiente y a
continuación sustituirla en otra ecuación por su valor.
En
caso de sistemas con más de dos incógnitas, la seleccionada debe ser sustituida
por su valor equivalente en todas las ecuaciones excepto en la que la hemos
despejado. En ese instante, tendremos un sistema con una ecuación y una
incógnita menos que el inicial, en el que podemos seguir aplicando este método
reiteradamente.
Por ejemplo, supongamos que queremos resolver por sustitución este sistema:
En la
primera ecuación, seleccionamos la incógnita { y} y por ser la de menor
coeficiente y que posiblemente nos facilite más las operaciones, y la
despejamos, obteniendo la siguiente ecuación.
y= 22-3I
El siguiente paso será sustituir cada ocurrencia de la incógnita {y} y
en la otra ecuación, para así obtener una ecuación donde la única incógnita sea
la {x}.
4.1 Igualación
El
método de igualación se puede entender como un caso particular del método de
sustitución en el que se despeja la misma incógnita en dos ecuaciones y a
continuación se igualan entre sí la parte derecha de ambas ecuaciones.
Tomando
el mismo sistema utilizado como ejemplo para el método de sustitución, si
despejamos la incógnita {y} y en ambas ecuaciones nos queda de la siguiente
manera:
Como
se puede observar, ambas ecuaciones comparten la misma parte izquierda, por lo
que podemos afirmar que las partes derechas también son iguales entre sí.
4.2 Reducción
Este
método suele emplearse mayoritariamente en los sistemas lineales, siendo pocos
los casos en que se utiliza para resolver sistemas no lineales. El
procedimiento, diseñado para sistemas con dos ecuaciones e incógnitas, consiste
en transformar una de las ecuaciones (generalmente, mediante productos), de
manera que obtengamos dos ecuaciones en la que una misma incógnita aparezca con
el mismo coeficiente y distinto signo. A continuación, se suman ambas
ecuaciones produciéndose así la reducción o cancelación de dicha incógnita,
obteniendo así una ecuación con una sola incógnita, donde el método de
resolución es simple.
Por ejemplo,
en el sistema:
No
tenemos más que multiplicar la primera ecuación por {-2} para poder cancelar la
incógnita {y}. Al multiplicar, dicha ecuación nos queda así:
El
siguiente paso consiste únicamente en sustituir el valor de la incógnita {x} en
cualquiera de las ecuaciones donde aparecían ambas incógnitas, y obtener así
que el valor de {y} si sustituimos en la primera ecuación es igual a:
5.
Método gráfico
Consiste
en construir la gráfica de cada una de las ecuaciones del sistema. El método
(manualmente aplicado) solo resulta eficiente en el plano cartesiano, es decir
para un espacio de dimensión.
El proceso de resolución de un
sistema de ecuaciones mediante el método gráfico se resuelve en los siguientes
pasos:
1.
Se despeja la incógnita en ambas ecuaciones.
2.
Se construye para cada una de las dos ecuaciones
de primer grado obteniendo la tabla de valores correspondientes.
3.
Se representan gráficamente ambas rectas en los
ejes coordenados.
4.
En este último paso hay tres posibilidades:
1.
Si ambas rectas se cortan, las coordenadas del
punto de corte son los únicos valores de las incógnitas (x,y). "Sistema
compatible determinado".
2.
Si ambas rectas son coincidentes, el sistema
tiene infinitas soluciones que son las respectivas coordenadas de todos los
puntos de esa recta en la que coinciden ambas. «Sistema compatible indeterminado».
3.
Si ambas rectas son paralelas, el sistema no
tiene solución en los reales, pero sí en los complejos.
6. MÉTODO DE GAUSS
El
método de eliminación de Gauss o simplemente método de Gauss consiste en
convertir un sistema lineal de n ecuaciones con n incógnitas, en uno
escalonado, en el que la primera ecuación tiene n incógnitas, la segunda
ecuación tiene n - 1 incógnitas, ..., hasta la última ecuación, que tiene 1
incógnita. De esta forma, será fácil partir de la última ecuación e ir subiendo
para calcular el valor de las demás incógnitas.
7. Eliminación
de Gauss-Jordán
Una
variante de este método, denominada eliminación de Gauss-Jordán, es un método
aplicable únicamente a los sistemas lineales de ecuaciones, y consistente en
triangular la matriz aumentada del sistema mediante transformaciones
elementales, hasta obtener ecuaciones de una sola incógnita, cuyo valor será
igual al coeficiente situado en la misma fila de la matriz. Este procedimiento
es similar al anterior de reducción, pero ejecutado de manera reiterada y
siguiendo un cierto orden algorítmico.
8. Regla de Cramer
La regla de Cramer da una solución para sistemas compatibles
determinados en términos de determinantes y adjuntos dada por:
Donde
Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector
columna b. Para un sistema de dos ecuaciones y dos incógnitas:
La
regla de Cramer da la siguiente solución:
Nota:
Cuando en la determinante original det(A) el resultado es 0, el sistema indica
múltiples o sin coincidencia.
Algoritmos
numéricos
La
eliminación de Gauss-Jordán es un algoritmo numérico usado para una gran
cantidad de casos específicos, aunque posteriormente se han desarrollado
algoritmos alternativos mucho más eficientes. La mayoría de estos algoritmos
mejorados tienen una complejidad computacional de O(n²) (donde n es el número
de ecuaciones del sistema). Algunos de los métodos más usados son:
·
Para los problemas de la forma Ax = b, donde A
es una matriz de Toeplitz simétrica, se puede utilizar la recursión de Levinson
o alguno de los métodos derivados de este. Un método derivado de la recursión
de Levinson es la recursión de Schur, que es ampliamente usado en el campo del
procesamiento digital de señales.
·
Para los problemas de la forma Ax = b, donde A
es una matriz singular o casi singular, la matriz A se descompone en el
producto de tres matrices en un proceso llamado descomposición en valores
singulares.
Cuando
consideramos ecuaciones lineales cuyas soluciones son números racionales,
reales o complejos o más generalmente un cuerpo {K}, la solución puede
encontrarse mediante Regla de Cramer. Para sistemas de muchas ecuaciones la
regla de Cramer puede ser computacionalmente más costosa y suelen usarse otros
métodos más "económicos" en número de operaciones como la eliminación
de Gauss-Jordán y la descomposición de Cholesky. Existen también métodos
indirectos (basados en iteraciones) como el método de Gauss-Seidel.
Si el
cuerpo es infinito (como es el caso de los números reales o complejos),
entonces solo puede darse una de las tres siguientes situaciones:
·
El sistema no tiene solución (en dicho caso se
dice que el sistema está sobre determinado o que es incompatible)
·
El sistema tiene una única solución (el sistema
es compatible determinado)
·
El sistema tiene un número infinito de
soluciones (el sistema es compatible indeterminado).
9. OPERACIONES
DE MATRICES
Para obtener los elementos de
unas matrices se suman los elementos correspondientes A, B.
Determine
las raíces reales de f(x) = -25182x-90x2+44x5-8x4+0.7x5
Las
raíces de f(x)=-1+5.5x-4x2+0.5x3
9.1 Producto interno de matrices
Sea A
el vector reglón y B el vector de la columna entonces el producto interno como
A.B = a11b11+a12b21+…ani
bni.
Ejemplo
1) Sea el
vector reglón A, B el vector de la columna
Producto de vectores
problema
Realizar
las operaciones de la fila en toda la matriz aumentada de tal forma de la
matriz A se transformé en la matriz identidad y la matriz de identidad original
se convierta en la matriz inversa de A.
3x+5y=7
2x-y=
- 4
Encontrar
A-1
Problema
x-y+z=2
x+y+z=4
2x+2y-z=-4
Actividad 2.
Los
tres hijos de un granjero, Amy, Beth y Chad atienden tres puestos al lado de la
carretera durante los meses del verano. Un fin de semana, todos venden sandías,
calabaza amarilla y jitomates. Las matrices A y B tabulan la cantidad de libras
de cada uno de los productos vendidos por cada uno de los hijos en el sábado y
el domingo:
Sábado
|
|||
Amy
|
120
|
50
|
60
|
Beth
|
40
|
25
|
30
|
Chad
|
60
|
30
|
20
|
=
A
Domingo
|
|||
Amy
|
100
|
60
|
30
|
Beth
|
35
|
20
|
20
|
Chad
|
60
|
25
|
30
|
=
B
La
matriz C proporciona los precios por libra, en dólares, de cada tipo de
producto que venden:
Precios
por libra
|
|
Sandias
|
0.10
|
Calabazas
|
0.50
|
Jitomate
|
1.00
|
= C
Efectúe
las siguientes operaciones con las matrices e interprete los elementos en cada
resultado. a) AC b) BC c)
A + B d) (A+B) C
12. REGLA DE CRAMER
Esta
regla establece que cada incógnita de un sistema de ecuaciones lineales
algebraicas puede expresarse como una fracción de dos determinantes con
denominador d y con el numerador obtenido a partir de d, al reemplazar la
columna de coeficientes de la incógnita en cuestión por las constantes b1, b2…bn.
1(-4-8)
+1
A=1
Y=1
Z=4
13. DESCOMPOSICIÓN LU
Recordemos,
que una matriz regulara, admite una factorización de la forma
PA=LU
Donde p
es una matriz de permutación de filas, L es una matriz triangular inferior y u es
una matriz triangular superior.
y sea
el sistema de ecuaciones [a][x]=[b]
Aunque
la eliminación gauss representa una forma satisfactoria para resolver tales sistemas,
resúltate y eficiente cuando deben resolver ecuaciones con los mismos coeficientes[a],
pero con diferentes constantes del lado derecho (las b).
Los
métodos de descomposición LU separan el tiempo usado en las eliminaciones para
la matriz [a] de las manipulaciones en el lado derecho {b}. una vez que [a] se
ha “descompuesto”, los múltiples vectores del lado derecho {b} se pueden
evaluar de manera eficiente.
UNA
ESTRATEGIA DE DOS PASOS
1.
paso de descomposición lu. [a] se factoriza o “descompone” en las matrices
triangulares inferior [l] y superior [u].
2.
paso de la sustitución. [l] y [u] se usan para determinar una solución {x} para
un lado derecho {b}. este paso, a su vez, se divide en dos. primero, la
ecuación [l][d]=[b], se usa para generar un vector intermedio {d} mediante
sustitución hacia adelante. después, el resultado se sustituye en la
ecuación[l][x]-[d]=0, la que se resuelve por sustitución hacia atrás para {x}.

X1= 5/4
X2= 5/2
X3=-3/20
14. Método de Gauss-Seidal
Actividad
3x1-0.1x2-0.2x3=7.85
0.1x1+7x2-0.3x3=-19.3
0.3x1-0.2x2+10x3=71.4
i
|
X1
|
Y2
|
Z3
|
Error x1
|
Error x2
|
Error x3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1.75
|
-0.9
|
1.68833
|
|||
2
|
1.93125
|
1.9825
|
1.42347
|
0.09
|
1.45
|
0.18
|
3
|
3.27505
|
2.36410
|
6.829
|
0.01
|
0.16
|
0.22
|
4
|
3.61792
|
2.74457
|
1.90102
|
0.09
|
0.14
|
0.04
|
5
|
3.83517
|
2.87468
|
1.95898
|
0.06
|
0.09
|
0.03
|
6
|
3.92196
|
2.94917
|
1.98019
|
0.02
|
0.02
|
0.01
|
7
|
3.96462
|
2.97392
|
1.99442
|
0.01
|
0.01
|
0.007
|
8
|
3.98489
|
2.99061
|
1.99601
|
0.005
|
0.005
|
0.0007
|
Actividad
17x-2y-3z=500
-5x-21y2z=200
-5x-5y+22z=30
15. MATRICES Y SISTEMAS DE ECUACIONES LINEALES
COMPETENCIA
Implementar los
métodos numéricos de solución de sistemas de ecuaciones lineales en la solución
de problemas de la ingeniería
15.1. SUMA DE MATRICES
Para
sumar dos matrices a y b han de ser de las mismas dimensiones; si esto es
cierto, la suma es una matriz e de iguales dimensiones que a y que b, y sus
elementos se obtienen sumando los elementos correspondientes de a y b.}
15.3. MULTIPLICACIÓN DE MATRICES
Dos
matrices a y b son conformes en ese orden (primero a y después b ), si a tiene
el mismo número de columnas que b tiene de filas.
Método de Gauss-Seidal
Actividad
3x1-0.1x2-0.2x3=7.85
0.1x1+7x2-0.3x3=-19.3
0.3x1-0.2x2+10x3=71.4
VECTORES
SISTEMAS EQUIVALENTES
Dos sistemas
de ecuaciones lineales son equivalentes si tienen exactamente las mismas
soluciones.
Transformaciones
que convierten un sistema en otro equivalente:
I.
Multiplicar o dividir ambos miembros de una ecuación por un número distinto de
cero.
II. Sumar
a una ecuación del sistema otra ecuación del mismo.
III. Eliminar
una ecuación que es combinación lineal de otras dos.
Un sistema equivalente y escalonado, mediante
transformaciones adecuadas.
Se
pueden dar los siguientes pasos:
I.Si
es necesario reordenar ecuaciones para que a11sea distinto de cero.
II.Dividir
la primera ecuación por a11y restar a cada ecuación un múltiplo de la primera
para eliminar todos los elementos que quedan por debajo de a11x1.
III.Repetir
los pasos anteriores basados ahora en a22(y si es necesario en cada aii).
IV.El
proceso termina cuando no quedan más ecuaciones.
16.
Para
concluir con este blog podemos precisar que los métodos numéricos son de suma
importancia en la resolución de problemas, nos sirven en muchas de las
ocasiones pues son capaces de aplicarse en sistemas de ecuaciones con una
magnitud considerable que analíticamente son mucho más complejas. Un gran
factor de los métodos números es que son aplicables en distintas ramas y
aspectos, pero más sin embargo no siempre se encuentra el resultado más óptimo
pues todos son valores con su grado de aproximación.
17. BIBLIOGRAFÍA
-APUNTES DEL CURSO DE MÉTODOS
NUMÉRICOS 2018, PROFESORA LORENA ALONSO GUZMÁN.
http://sauce.pntic.mec.es/~jpeo0002/Archivos/PDF/T07.pdf
http://www.sinewton.org/numeros/numeros/57/Articulo01.pdf
https://www.uv.es/lonjedo/esoProblemas/3eso6ecuaciones1grado.pdf
http://sauce.pntic.mec.es/~jpeo0002/Archivos/PDF/T07.pdf
http://www.sinewton.org/numeros/numeros/57/Articulo01.pdf
https://www.uv.es/lonjedo/esoProblemas/3eso6ecuaciones1grado.pdf

































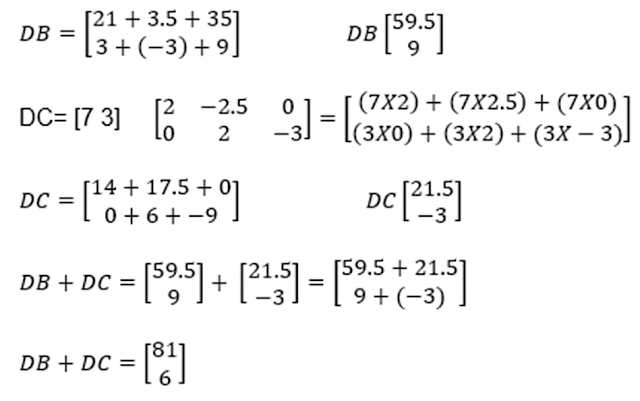


























No hay comentarios:
Publicar un comentario